
Developed by several Ph.D. students and post docs, under the guidance of
Timothy S. Cale
EVOLVE has the ability to simulate electrochemical deposition using its ECD module. The ECD module includes two finite element based solvers: the pseudo-steady state solver and the transient solver. Between these two solvers, a large fraction of possible electroplating situations can be addressed.
The pseudo-steady state (PSS) solver allows EVOLVE's ECD module to solve problems for which Poisson's equation applies to a stagnant film inside and around a feature or set of features. It is referred to as pseudo-steady because the species concentration fields and the electric field in the liquid phase come to equilibrium on a time scale much shorter than the time scale for surface evolution. We take advantage of this to speed up calculations.
Figure 1, below, shows the equations and boundary conditions that the PSS solver must deal with to calculate the deposition rate at the surface.

Figure 1: The computational domain in which the pseudo-steady state solver operates, and the equations and boundary conditions it solves to find the deposition rate.
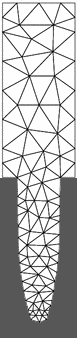
Figure 2: An example of an unstructured mesh the pseudo-steady state solver uses for its finite element calculation of the species concentration fields and the electric field.
The transient solver can be used whenever the pseudo-steady assumption does not hold. This is true for a variety of electroplating processes, including pulsed potential and depositions from baths in which additives accumumlate on the surface throught the deposition, such as for curvature enhance deposition [1, 2]. The transient solver solves Laplace's equation in the fluid phase, with appropriately varying boundary conditions, as shown in Figure 3 below.

Figure 3: The computational domain in which the pseudo-steady state solver operates, and the equations and boundary conditions it solves to find the deposition rate.
Figures 4 and 5 below show simulations results for 2 sets of 5 identical trenches with an aspect ratio of 2 for a modern 3-component bath with additives to promote bottom up filling. The only difference in the intial structures is the inter-trench spacing, but this clearly makes an difference on the final deposited structure. These pattern density effects can make in impact on post-ECD processing.


Figure 5: A set of five aspect ratio 2 idealized trenches after simulated electrochemical deposition using a bath containing both an accelerator and a suppressor species. The inter-trench spacing is equal to the trench width.
Please look at a presentation of how the transient solver can be used for a variety of purposes.